Sudoku

In sudoku is in puzel fan 9x9 fakjes mei in lyts oantal al ynfolde inkelfâldige sifers. De keunst is om de oare fakjes sá yn te foljen dat yn elke horizontale rige én yn elke fertikale kolom de sifers 1 o/m 9 ien keer foarkomme. Boppedat is de puzel ûnderferdield yn njoggen blokjes fan 3x3, dy't elk ek wer ienmel de sifers 1 o/m 9 befetsje moatte.
Tinkpuzel[bewurkje seksje | boarne bewurkje]
Oars as in soad oare puzels binne sudoku's op te lossen troch elk dy't ree is syn harsens in skoftke konsentreard te brûken en systematysk neitinke wol. Wiskundige kennis is net fereaske, omdat de symbolen gjin betsjutting hawwe, útsein dat se ferskillend binne. Oare symboalen kinne ek. Der binne ek sudoku's mei letters, en ek mei sifers én letters tagelyk.
De swierrigensgraad fan in opjefte hinget, oars as faaks sein wurdt, net echt ôf fan it tal ynfolde sifers. In opjefte mei 19 gegevens kin hiel ienfâldich wêze en ien mei 36 gegevens hiel slim. (By it samar generearjen fan opjeften mei 19 gegevens liket it oantal slimme puzels sels wat leger as by 24 gegevens.) Der binne sudoku's bekend mei 17 gegevens (en in unike oplossing), mar oant no ta net mei 16 gegevens.
Puzelmeitsje mei in kompjûter[bewurkje seksje | boarne bewurkje]
By it meitsjen fan in opjefte moat it kompjûterprogramma earst in oplossing generearje middels willekeurige ferdielingen fan de 9 sifers en toetsing fan de rige-kolom-blok-kompatibiliteit. Sa gau at in nije oplossing fûn is, moat se omsetten wurde nei in opjefte troch der (ek willekeurig) in oantal sifers fan frij te jaan. It kompjûterprogramma moat dan neigean oft de frijjûne sifers mar ien inkele oplossing talitte. Is dat net sa, dan kin in bykommend sifer frijjûn wurde (en hieltiten wer ien folgjend), oant de puzel mar op ien manier op te lossen is. Kompjûterprogramma's dy't in útfigelearre oplossingsstrategy brûke binne dêrtroch by steat slimmere puzels te produsearjen want se moatte minder hurd in sifer frijjaan. Sa komt it foar dat puzels mei net mear as 25 (of inkeldris 240 frijjûne sifers produsearre wurde kinne. Mar al by al kinne dy soms makliker wêze as in 26-sifer-kombinaasje omdat dêr tafallichredundante frijjûn binne.
Untstean[bewurkje seksje | boarne bewurkje]
De puzel is betocht troch Howard Garns, in pensjonearre arsjitekt en freelance puzelmakker en waard foar it earst publisearre yn 1979 ûnder de namme Number Place. De puzel waard yn 1984 troch Nikoli yn Japan yntrodusearre dêr't it ek de namme sudoku (gearfoeging fan 'Suuji wa dokushin ni kagiru' krige. Dat betsjut dat it beheind is ta ûnôfhinklike, "net-troude", getallen. 'su' betsjut getal, 'doku' betsjut ûnôfhinklik, net-troud. Fanôf 1986 wie sudoku populêr yn Japan. Yn 1997 seach Wayne Gould, in Nij-Seelânske pensjonearre, in sudoku. Hy wurke dêrnei 6 jier oan in kompjûterprogramma om sudoku's op te stellen. Hy ferkocht de hiele saak oan The Times dy't op 12 novimber 2004 begûn mei it publisearjen fan de puzels. In nije raazje wie berne. Yn de simmer fan 2005 waard de puzel ek yntrodusearre in Nederlân en waard al gau populêr, ûnder mear omdat in soad kranten alle dagen in sudoku pleatsten. Op 15 oktober 2005 waarden de earste Nederlânske kampioenskippen sudoku holden yn it Skipfeartmuseum yn Amsterdam. Delia Keetman út Heerhugowaard waard earste..
Oplossen[bewurkje seksje | boarne bewurkje]
Oplostrategy 1[bewurkje seksje | boarne bewurkje]
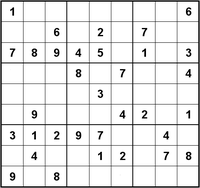
Nim as foarbyld de lege puzel hjirboppe.

Stap 1[bewurkje seksje | boarne bewurkje]
- Sykje in rige mei net te folle lege fakjes. Yn dit gefal de 3e rige fan boppe.
- De getallen dy't yn dy rige noch misse binne 2 en 6.
- De 2 kin net yn it earste lege hokje stean, omdat yn dizze kolom al in 2 stiet.
- De 2 moat dus yn it lêste lege hokje stean.

Stap 2[bewurkje seksje | boarne bewurkje]
- Omdat no allinnich de 6 noch ûntbrekt yn dizze rige, kin ek dy sa ynfolle wurde.

Stap 3[bewurkje seksje | boarne bewurkje]
- Yn it blok linksûnder ûntbrekke noch de 5, de 6 en de 7. Nim bygelyks de 7.
- De 7 kin net yn de boppeste 2 rigen (fan it blokje!) stean, omdat yn dy rigen al in 7 stiet.
- De 7 kin ek net yn de earste kolom stean, want dêr stiet ek al in 7.
- Ek kin de 7 net rjochtsûnder stean, want dêr stiet al in 8.
- De 7 moat dus wol ûnder yn 'e midden.

Stap 4[bewurkje seksje | boarne bewurkje]
- No ûntbrekke yn dit blok allinnich de 5 en de 6 noch.
- De 6 kin net yn de rjochterkolom, omdat dêryn al in 6 stiet.
- De 6 moat dus yn it fakje linksmidden.

Stap 5[bewurkje seksje | boarne bewurkje]
- Allinnich de 5 yn it blok linksûnder mist noch, dizze moat dus yn it fakje rjochtsmidden.
Oplosstrategy 2[bewurkje seksje | boarne bewurkje]
As de opjeften slimmer binne, binne der meastal gjin rigen dy't al hast kompleet ynfold binne. Dan is bygelyks dizze strategy handich:
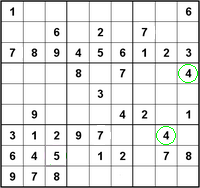
Stap 1[bewurkje seksje | boarne bewurkje]
Sykje yn in rige fan trije blokken (horizontaal of fertikaal) twa blokken mei itselde symboal. Bygelyks de 4-en yn de rjochter fertikale rige.
Stap 2[bewurkje seksje | boarne bewurkje]
Elk symboal komt ien kear yn elk blok en yn elke rige foar. It blok rjochtsboppe mist noch in 4. De 4 past logyskerwize allinnich yn de earste kolom. Yn dy kolom is noch ien mooglikheid iepen.
Ferfolch[bewurkje seksje | boarne bewurkje]
Merkbyt dat no yn de earste horizontale rige fan trije blokken, twa blokken in 4 krigen hawwe. Yn it blok linksboppe moat in 4 komme op de middelste rigel. Troch de 4 , dy't yn it blok linksûnder stiet, kin dy mar op ien plak ynfold wurde.
En fierder[bewurkje seksje | boarne bewurkje]
Meitsje sels de rest fan de puzel ôf. Noch inkele tips:
- Konsintrearje op ien sifer, bygelyks in sifer dat al faak foar komt.
- Begjin mei in blok, rige of kolom dy't al hast fol is.
- Bliuw de strategyen werheljen. Alle kearen at in sifer ynfold is bliuwe der minder mooglikheden oer.
- Jo kinne oantekenings meitsje: de mooglike getallen foar in hokje tin der yn sette. Sa gau at earne oars yn 'e kolom of rige ien fan dizze getallen ynfolle wurdt, kin it yn dat hokje weistreke wurde. Sa bliuwt der úteinlik ien mooglikheid oer.
Farianten[bewurkje seksje | boarne bewurkje]

Soms is it sa dat de diagonalen ek de sifers 1 o/m 9 befetsje, dit hjit in X-sudoku. Ek is der in spulfariant wêrby't de skean oan inoar buorjende fakjes nea deselde getallen befetsje.
Der binne ek puzels besteande út 5 klassike sudoku's wêrby't dizze fiif puzels (ien sintrale en ien yn elke hoeke) yn inoar heakke binne: it rjochterûnderblok fan 'e puzel linksboppe is bygelyks deselde as it linkerboppeblok fan de sintrale sudoku.
Der bestiet ek in fariant fan sudoku dêr't it giet om in fjild fan 6x6 hokjes. Hjirby wurde de getallen 1 o/m 6 ynfold yn alle rigen, kolommen en fakjes.
De Sudoku dy't alle wiken yn NRC Handelsblêd stiet, wurket as in normale Sudoku, mar hat as bykommende swierrichheid dat hy 4 ekstra flakken fan 3x3 befettet, dy't ek fold wurde moatte mei de sifers 1 o/m 9. Dizze fjouwer oerlaapje folslein mei de 9 flakken fan de basis-Sudoku: de ôfmjittings binne gewoan 9x9.
Der is ek in sudoku dy't bestiet út 16 fakken fan elk 4 by 4. De rjochte linen (horizontaal en fertikaal) foarmje elk in rige fan 16. Dizze foarm fan sudoku wurket mei heksadesimale symbolen, dit wol sizze fan 0 o/m F. Dizze foarm wurdt ek wolris in heksadoku neamd. Fieders is der in foarm fan 25 fakken fan 5 x 5. Dizze sanaamde alfadoku befettet de letters A o/m Y.
Noch in fariant is de saneamde foarmsudoku. Hjirby moatte lykas by de gewoane sudoku yn elke rige, kolom en elk blokje de sifers ien oant en mei njoggen ien kear foar komme, mar hawwe de blokjes in oare foar as 3x3.
Fierders is der noch de Killer Sudoku (ek bekend as Som-Sudoku of samunamupure). Dit is in puzel dêr't eleminten fan sudoku en kakuro gearfoege binne.
In somsudoku bestiet ek, dêr stean dan mallen op it fjouwerkant mei in getal deryn: de som fan de sifers.
Sudoku-spulkompjûter[bewurkje seksje | boarne bewurkje]
Fanwege de populariteit fan sudoku's binne sudokuspulkompjûters op de merk ferskynd. De prizen fan de spulkompjûters fariearje. De systemen fan de spulkompjûters ferskille: de ien hat pylkjetoetsen en in numeryk toetseboerd, de oar hat in PDA-eftich systeem.
Sjoch ek[bewurkje seksje | boarne bewurkje]
- Japanske puzel
- Oplossingsskema Sudoku
- In platfoarm foar ynternasjonaal meidwaan yn sudoku. Ek te krijen yn sudoku yn Nederlânske taal.
